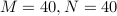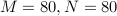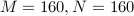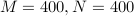Homotopy OpTimization ML (HOTML) and DeepHOTML detectors

The archive provided in this page contains ready-to-use binaries and MATLAB functions for the HOTML and DeepHOTML detectors. The binaries and functions can be freely distributed for academic or personal use. Please contact the authors if you intend to employ the binaries or functions in the archive for commercial purpose.

Source Code

The HOTML detector is written using MATLAB; the DeepHOTML network is written using the tensorflow package and tested using MATLAB.

DeepHOTML Detector

The maximum-likelihood (ML) MIMO detection problem with binary constellation is given by

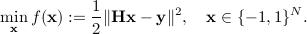
The two building blocks leading to our methods for handling the ML detection problem above are a homotopy transformation and an efficient first-order method.

with a parameter 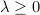lambdageq 0

. For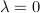

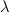, the problem is a convex relaxation of the ML problem (easy to solve); for a larger lambda

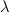, the problem is, intuitively, closer to the ML problem but is more non-convex (harder to solve). The idea of homotopy optimization is to try to find the ML solution by trying to trace the solution path of a sequence of the transformed problems, from small lambda

to large

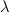Second, the homotopy-transformed problem is handled by an efficient first-order method and its deep-unfolded adpatation — named HOTML and DeepHOTML, respectively. HOTML employs a combination of majorization-minimization and the accelerated projected gradient method. Simply speaking, it takes a recursive form

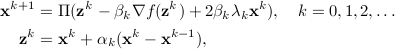
$begin{aligned} mathbf x^{k+1} = &~ Pi(mathbf z^k - beta_k nabla f(mathbf z^k)+ 2 beta_klambda_kmathbf x^k), quad k=0,1,2,ldots mathbf z^k =&~ mathbf x^k +alpha_k(mathbf x^k -mathbf x^{k-1}), end{aligned}$

where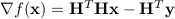

nabla f(mathbf x) = mathbf H^T mathbf H mathbf x - mathbf H^T mathbf y

is the gradient of

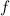is the projection onto [-1,1]^N

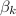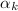is a step size, alpha_k

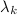is an extrapolation coefficient, and lambda_k

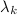increases gradually. DeepHOTML maps the iterations of HOTML as layers of a deep neural network, with the homotopy parameter lambda_k

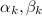and several other parameters (e.g., alpha_k, beta_k

) learnt from training data. The following diagram shows one layer of the DeepHOTML network, with four scalar trainable parameters marked as {color{red} mbox{red}}

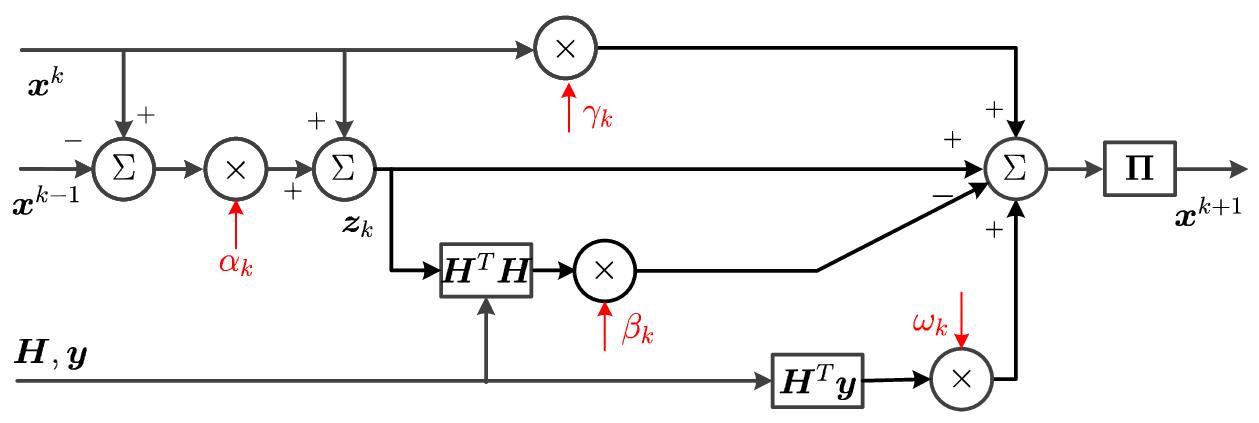The DeepHOTML/HOTML can also handle the one-bit ML MIMO detection problem; that is, the received signal 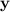mathbf y

is one-bit quantized. For more details, please see the following paper

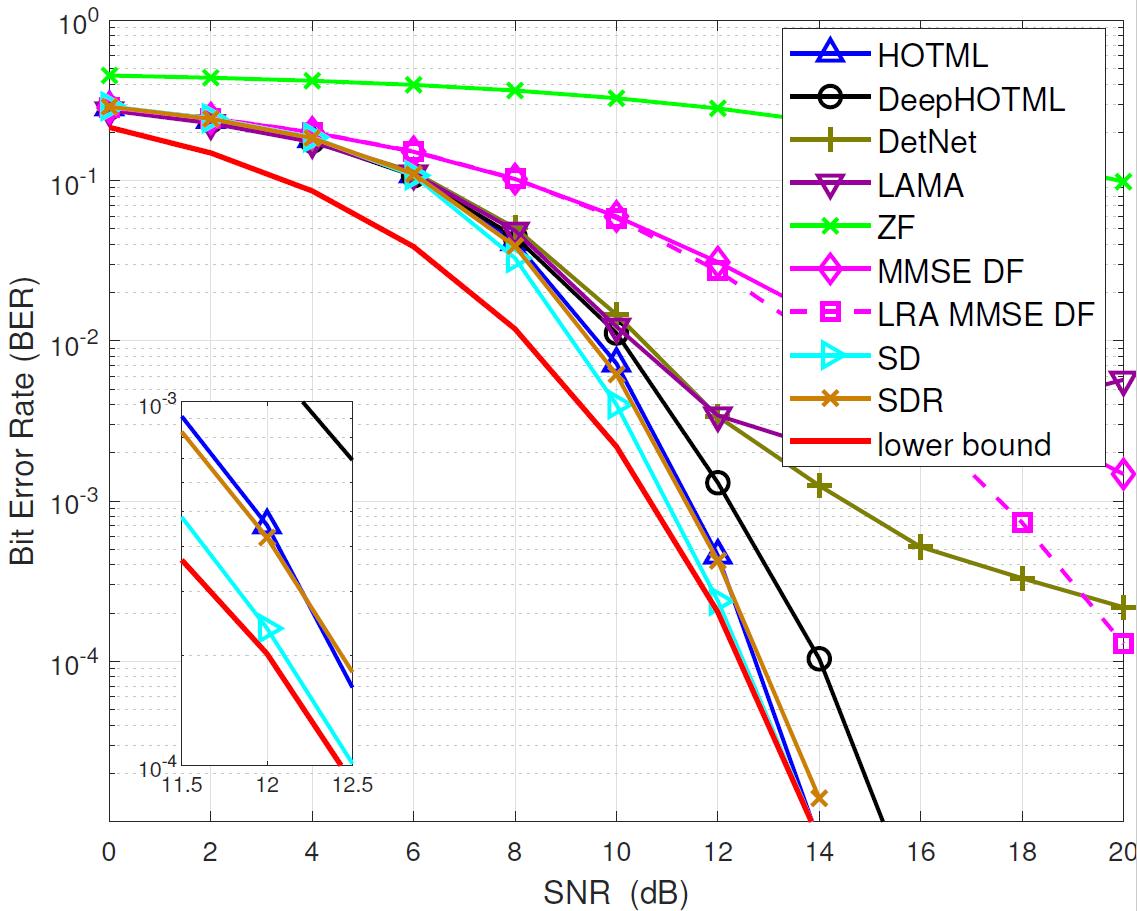
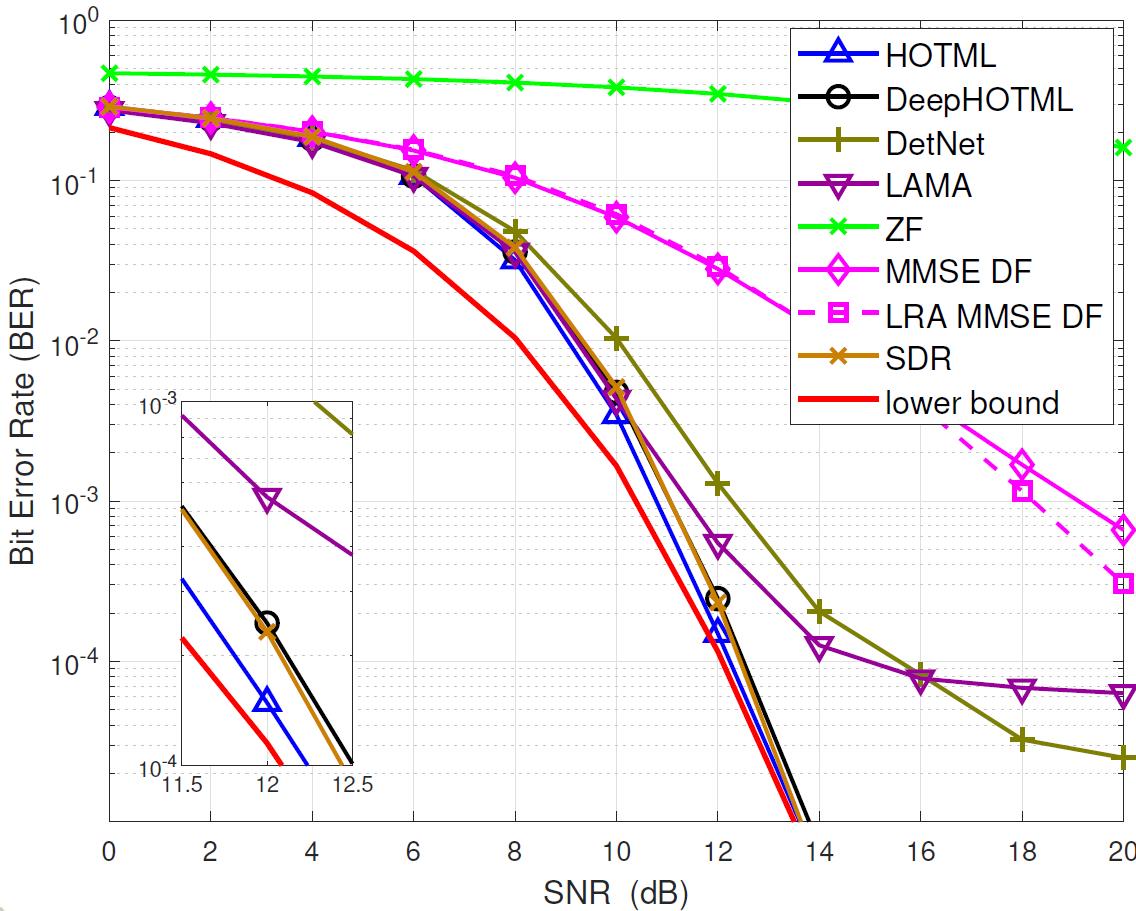
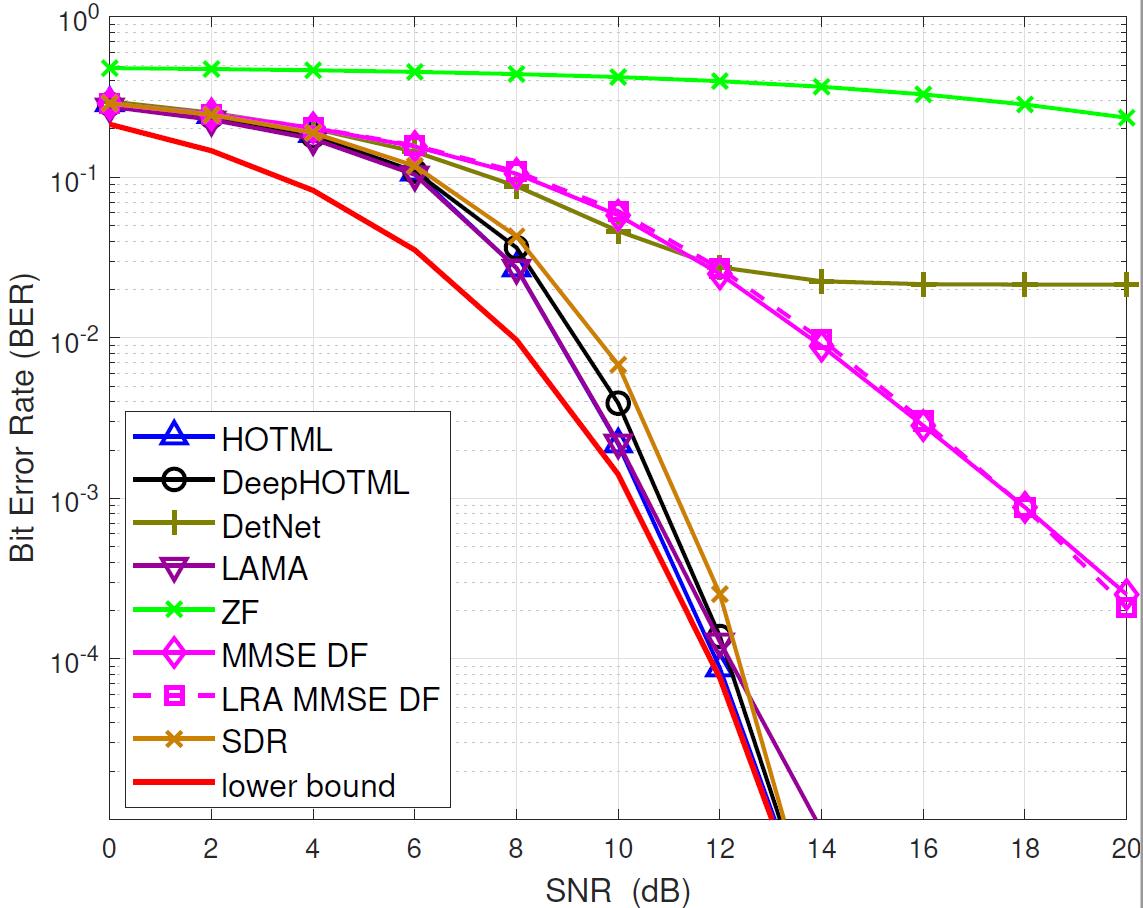
Simulations

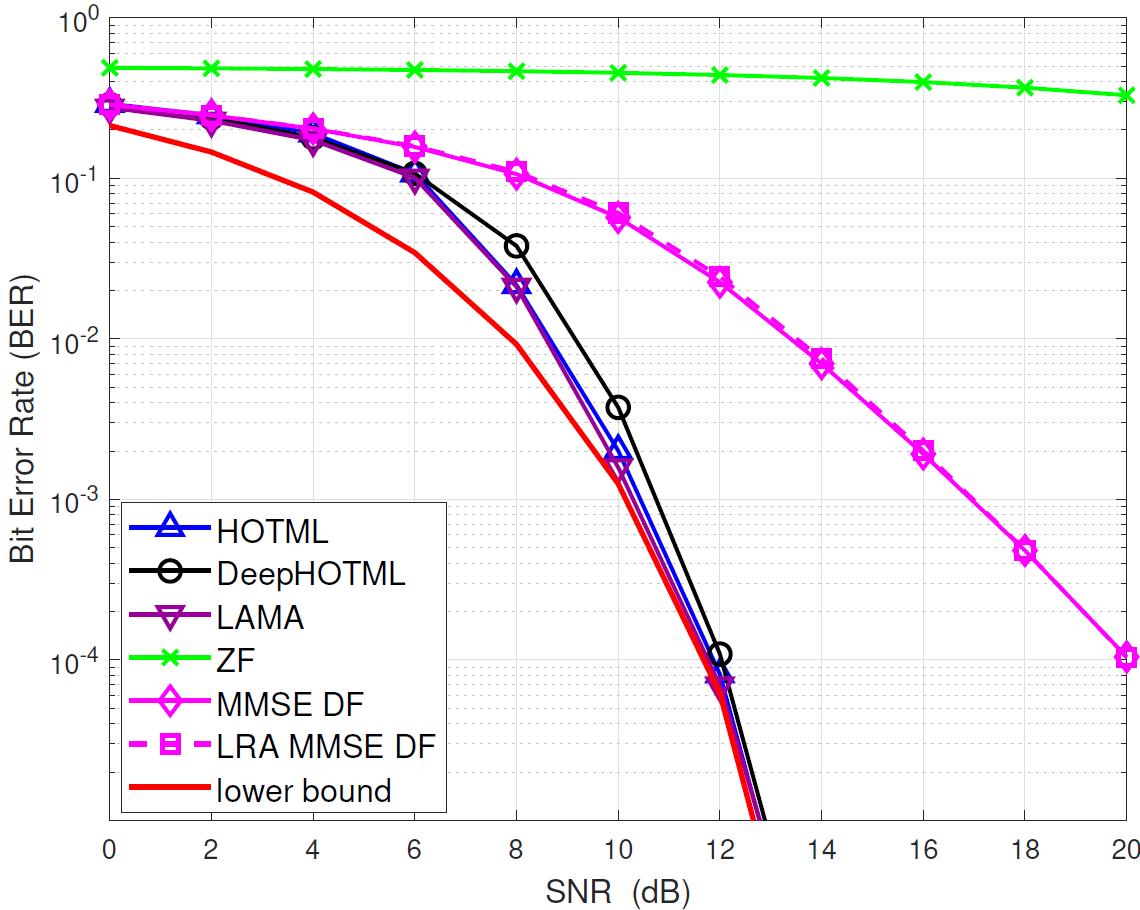
We demonstrate the performance of the DeepHOTML/HOTML detector for different problem sizes (in real dimension).

In the figures below,

'ZF’ denotes the zero-forcing detector,
'MMSE DF’ denotes the minimum-mean-square-error decision-feedback detector,
'LRA MMSE DF’ denotes the lattice reduction-aided MMSE DF detector,
'SD’ denotes the sphere decoder with Schnorr-Euchner implementation,
'SDR’ denotes the semidefinite relaxation, implemented by the row-by-row method,
'DetNet’ denotes the detection network, see here,
'LAMA’ denotes the large MIMO approximate message passing, see here.