Prof. Thierry Blu
FIEEE, FHKIE
News
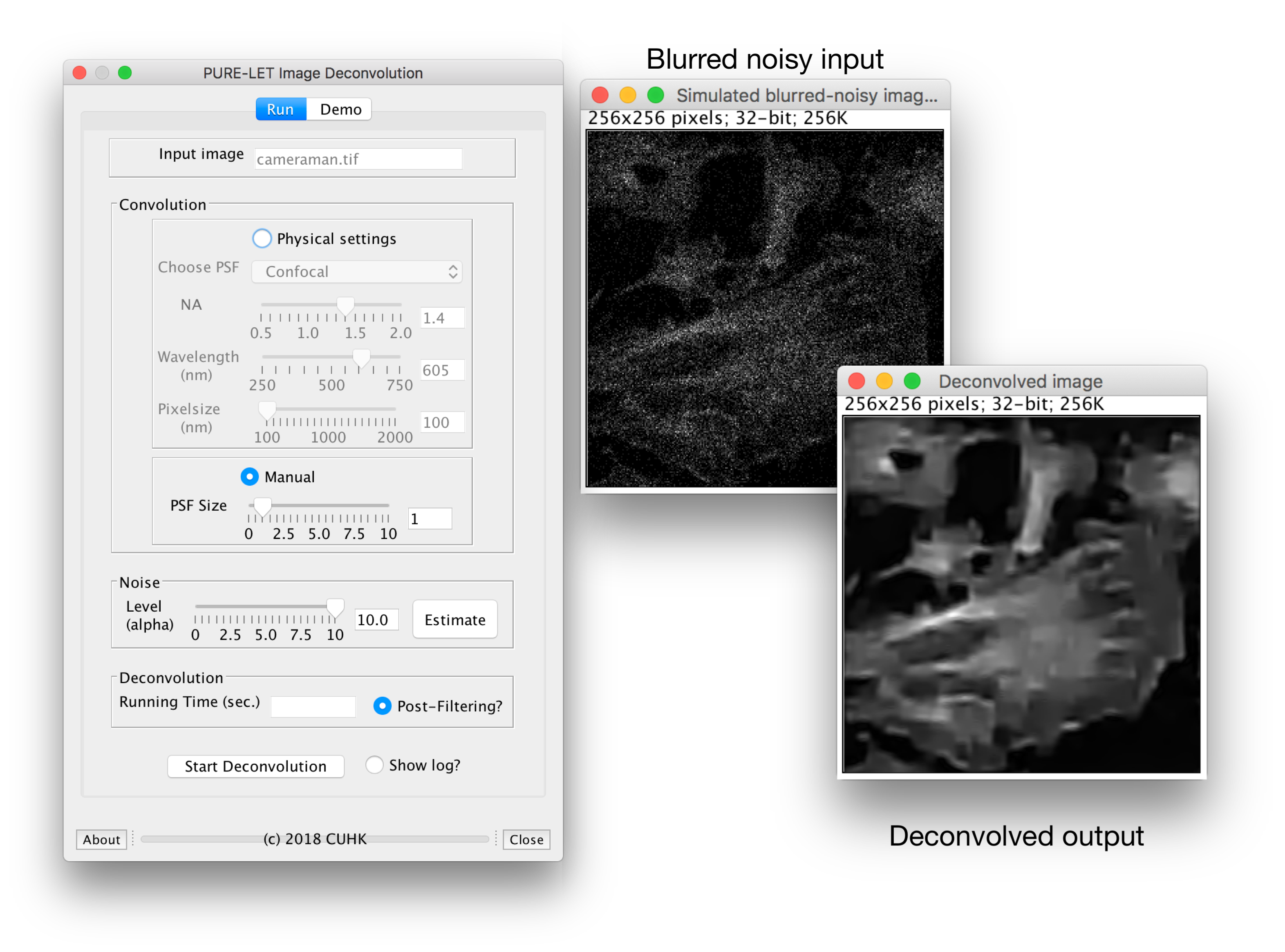
PURE-LET Image Deconvolution
Jizhou Li, Florian Luisier and Thierry Blu
Outline
In a variety of applications, ranging from astronomical imaging to biological microscopy, the predominant source of noise follows a Poisson distribution due to the quantum nature of the photon-counting process at the detectors. The observation model for a linear degradation caused by blurring and Poisson noise (and possibly additive Gaussian noise) is given by
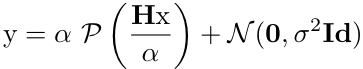
where 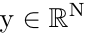 denotes the distorted observation of the unknown true image
denotes the distorted observation of the unknown true image 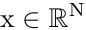 ,
, 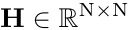 expresses a convolution with the point spread function, and N is the total number of pixels of the image.
expresses a convolution with the point spread function, and N is the total number of pixels of the image. 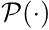 represents the effect of Poisson noise.
represents the effect of Poisson noise.
Our approach is to approximate the deconvolution process as a linear combination of elementary processings of the image, termed "linear expansion of thresholds (LET)" whose coefficients are obtained by minimizing a quadratic criterion (the Poisson unbiased risk estimate — PURE). Each elementary processing consists of Wiener/Tikhonov filtering followed by adaptive thresholding in the wavelet domain. The principle is shown as follows:

Advantages of the proposed approach:
- Non-iterative and thus has an explicit solution.
- Low computational complexity since it boils down to solving a small linear system of equations.
- Very robust to a wide range of noise level.
- No parameter tuning.
References
| [1] Li, J., Luisier, F., & Blu, T.,"PURE-LET image deconvolution", IEEE Transactions on Image Processing, Vol. 27 (1), pp. 92–105, January 2018. |
| [2] Li, J., Luisier, F., & Blu, T.,"PURE-LET deconvolution of 3D fluorescence microscopy images", Proceedings of the Fourteenth IEEE International Symposium on Biomedical Imaging (ISBI'17), Melbourne, Australia, pp. 723–727, April 18–21, 2017. Best student paper award (2nd place). |
| [3] Li, J., Luisier, F., & Blu, T.,"Deconvolution of Poissonian images with the PURE-LET approach", Proceedings of the 2016 IEEE International Conference on Image Processing (ICIP'16), Phoenix, AZ, USA, pp. 2708–2712, September 25–28, 2016. Best Paper Runner-Up Award. |
Software for download
- The Matlab code implementing the 2D PURE-LET image deconvolution algorithm is available here (69KB). Details on how to use this software: README2D.txt.
- The Matlab code implementing the 3D PURE-LET image deconvolution algorithm is available here (6MB). Details on how to use this software: README3D.txt
- The ImageJ plugin implementing the 2D PURE-LET image deconvolution algorithm is available here (5.6MB). Installation details: readmeImageJ.txt.
ImageJ plugin snapshot