Super-resolving a frequency band

Ruiming Guo and Thierry Blu

Outline

Estimating the frequency of a signal is a classical problem, and finds applications in the processing of signals from, inter alia, radars, sonars, NMR (Nuclear Magnetic Resonance) spectrometers, seismographs. The textbook approach for solving this problem involves the calculation of the Fourier transform of the signal considered.

Infinite frequency resolution is apparently out of reach, though, owing to Heisenberg's uncertainty, and this is somewhat confirmed by the intrinsic sampling step, 2π/N, of the Discrete Fourier Transform (DFT). Or is it really so?

In fact, infinite accuracy can be achieved by using as few as two DFT coefficients; i.e., the Discrete-Time Fourier Transform evaluated at two frequencies ω₁, ω₂, that are separated by 2π/N (or a multiple of it). More surprisingly, the phase of these two coefficients does not even matter. The simple formula that makes this feat possible is displayed in the figure below (X(ω) is the DTFT of the signal)

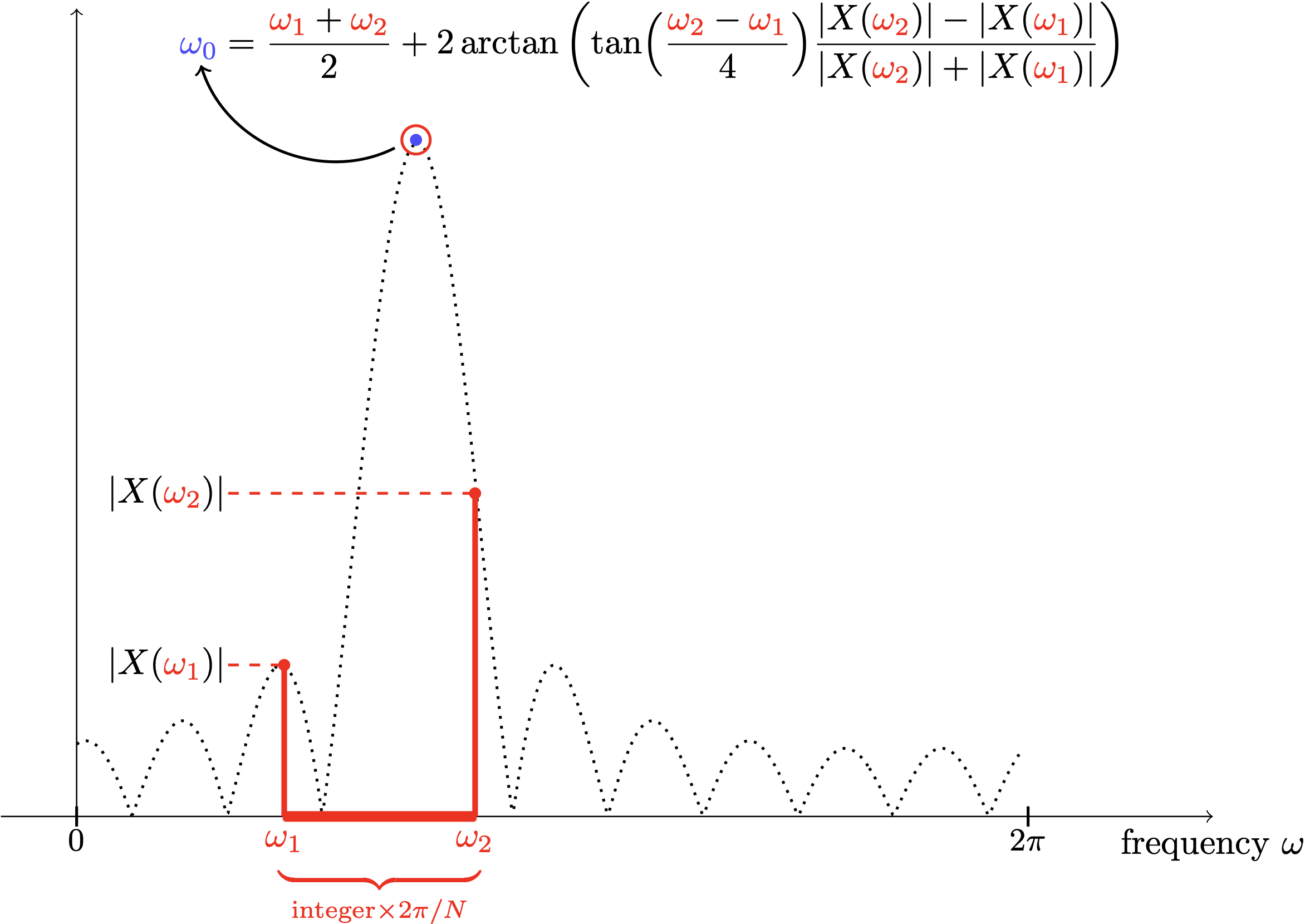
In the presence of noise, a double application of this formula (see [1] for details) provides an estimate whose inaccuracy is roughly equal to the Cramér-Rao theoretical minimum—a difference of less than 1%.

By identifying the most significant local maxima of the DFT (e.g., using the findpeaks function in MatLab), this formula can easily be used to deal with multiple frequencies. Typical result (5 frequencies, 30 samples):

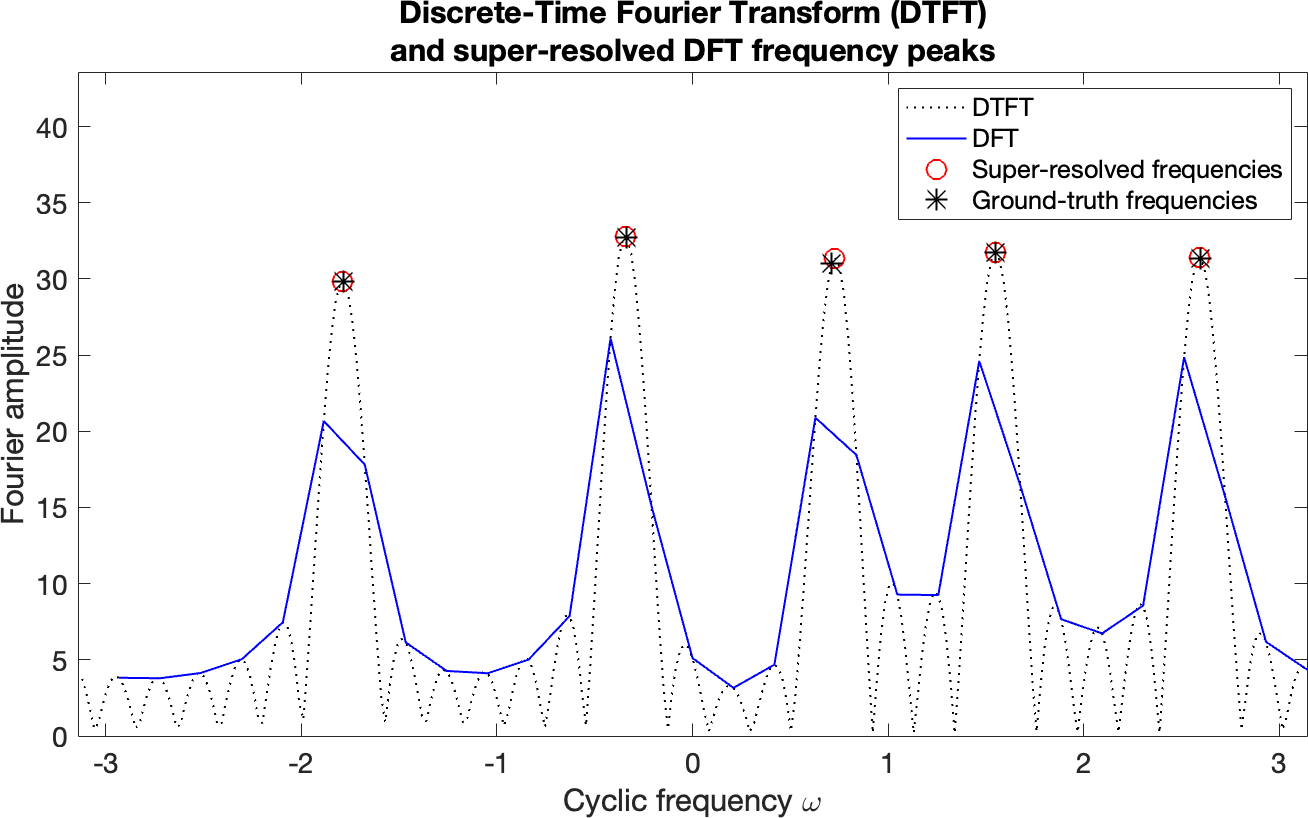
where the errors with the ground-truth frequencies range from 0.3% to 6% of the DFT bin size (2π/30). The downloadable MatLab software below can be used to test this "cheap" super-resolution approach more extensively.

References

[1] Guo, R. & Blu, T.,"Super-Resolving a Frequency Band", IEEE Signal Processing Magazine (2023). To appear.

Software for download

• The Matlab code implementing the super-resolution frequency retrieval is available here (7KB). Details on how to use this software: readme.txt.

Conditions of use — You are free to use this software for research purposes, but you should not redistribute it without our consent. In addition, we expect you to include an adequate citation and acknowledgment whenever you present or publish results that are based on it.