Prof. Thierry Blu
FIEEE, FHKIE
News
Multi-Wiener SURE-LET Deconvolution
Feng Xue, Florian Luisier and Thierry Blu

Outline
We extend the SURE-LET approach initially developed for image denoising, to image deconvolution. The deconvolution process is linearly parametrized by using multiple Wiener filters as elementary functions, followed by undecimated Haar-wavelet (subband-dependent) thresholding. Three key contributions make this approach novel, feasible, and even computationally efficient:
- The quality criterion to optimize is a statistical estimate of the Mean-Squared Error (MSE) of the full deconvolution process, which depends only on observed data (Stein's Unbiased Risk Estimate—SURE);
- The deconvolution process is parametrized as a linear combination of known elementary functions (Linear Expansion of Thresholds—LET);
- The use of several "Wiener" filterings with different (but fixed) regularization parameters.
A very interesting aspect of this approach is that the loss of degrees of freedom resulting from having fixed (non-linear) regularization parameters is totally compensated by the degrees of freedom brought by the (many) linear parameters.
References
| [1] Xue, F., Luisier, F. & Blu, T.,"SURE-LET image deconvolution using multiple Wiener filters", Proceedings of the 2012 IEEE International Conference on Image Processing (ICIP'12), Orlando, USA, pp. 3037-3040, September 30--October 3, 2012. |
| [2] Xue, F., Luisier, F. & Blu, T.,"Multi-Wiener SURE-LET Deconvolution", IEEE Transactions on Image Processing, Vol. 22 (5), pp. 1954-1968, 2013. |
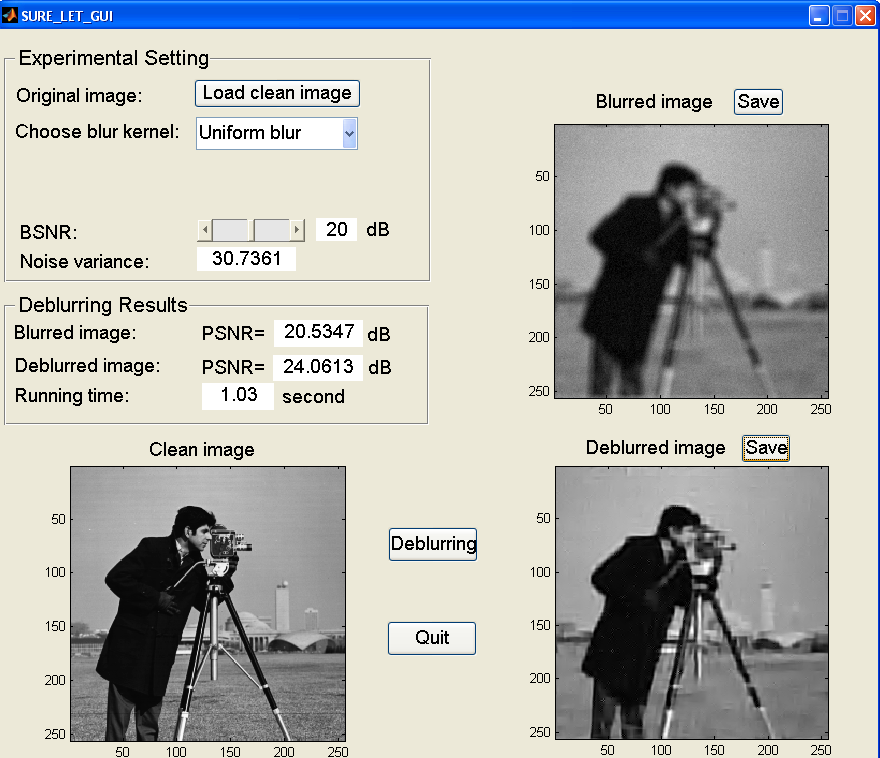
Matlab Software
The Matlab code available here is a demo of the algorithm described in the above papers. This package implements the multi-Wiener SURE-LET deconvolution. Download the zip archive. To understand how to use these files, please read the file README.txt or the online help in the routines.Demo snapshot