Prof. Thierry Blu
FIEEE, FHKIE
News
Iterative Linear Expansion of Thresholds (i-LET)
Hanjie Pan and Thierry Blu
Introduction
We focus on image restoration where the reconstructed image 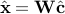 is found by minimizing an objective functional that consists of a quadratic data-fidelity term regularized with the standard sparsity-enforcing
is found by minimizing an objective functional that consists of a quadratic data-fidelity term regularized with the standard sparsity-enforcing 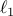 norm:
norm:
where 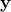 is the observation,
is the observation, 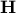 models the measurement process and
models the measurement process and 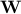 is some transformation, e.g. wavelet, such that
is some transformation, e.g. wavelet, such that 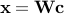 . We propose a novel algorithmic approach to solve this optimization problem iteratively. Our idea amounts to approximating the result of the restoration as a linear combination of basic thresholds (e.g. soft-thresholds) weighted by unknown coefficients at each iteration:
. We propose a novel algorithmic approach to solve this optimization problem iteratively. Our idea amounts to approximating the result of the restoration as a linear combination of basic thresholds (e.g. soft-thresholds) weighted by unknown coefficients at each iteration:
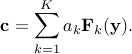
The few coefficients (typically less than 10) of this expansion are obtained by minimizing the equivalent low-dimensional 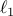 -regularized objective functional, which can be solved efficiently with standard convex optimization tools, e.g. iterative reweighted least squares (IRLS). We prove that, under simple conditions that the elementary thresholding functions should satisfy, global convergence of the iterated LET algorithm is guaranteed.
-regularized objective functional, which can be solved efficiently with standard convex optimization tools, e.g. iterative reweighted least squares (IRLS). We prove that, under simple conditions that the elementary thresholding functions should satisfy, global convergence of the iterated LET algorithm is guaranteed.

Figure 1: Iterative LET Scheme
Experiments on several test images over a wide range of noise levels and different types of convolution kernels clearly indicate that the proposed framework usually outperform state-of-the-art algorithms in terms of both CPU time and number of iterations.
References
| [1] Pan, H. & Blu, T.,"An Iterative Linear Expansion of Thresholds for $ell_1$-based Image Restoration", IEEE Transactions on Image Processing, Vol. 22 (9), pp. 3715-3728, September 2013. |
| [2] Pan, H., & Blu, T.,“Sparse Image Restoration Using Iterated Linear Expansion of Thresholds”, Proceedings of the 2011 IEEE International Conference on Image Processing (ICIP'11), Brussels, Belgium, pp. 1905-1908, September 11--14, 2011. |
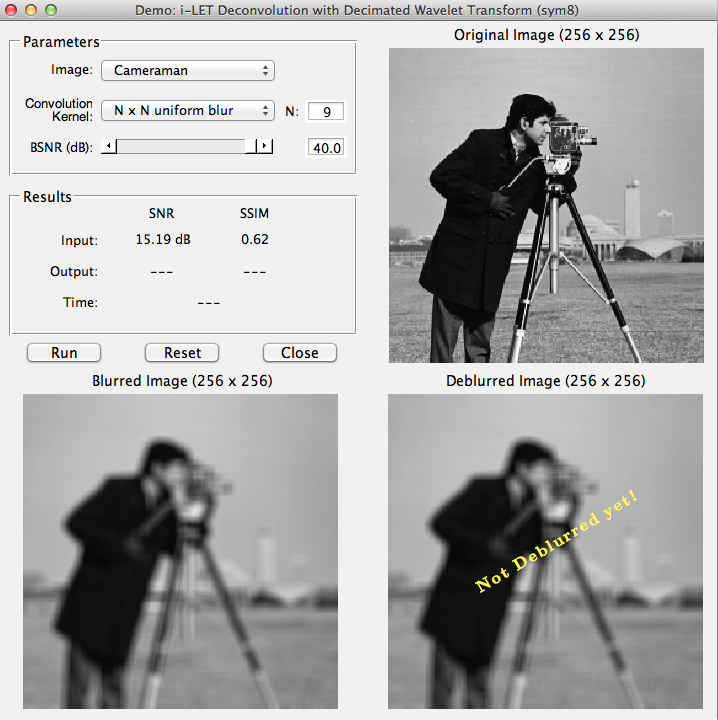
Matlab software
The Matlab implementation of the i-LET algorithm described in [1, 2] is available here (2.1MB). Please read the file README to understand how to start the demo.Demo snapshot