
Prof. Thierry Blu
FIEEE, FHKIE
News
Fourier-Argand Representation
Tianle Zhao and Thierry Blu
Outline
The solutions to many 2D signal processing problems rely on the identification of patterns (e.g. molecules in biological imagery) or local structures (e.g. edges/ridges in general) that could appear with arbitrary orientations.
Our method of study is to consider an optimal linear approximation problem, where we simultaneously approximate a given square-integrable function 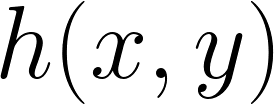 together with all of its rotations
together with all of its rotations 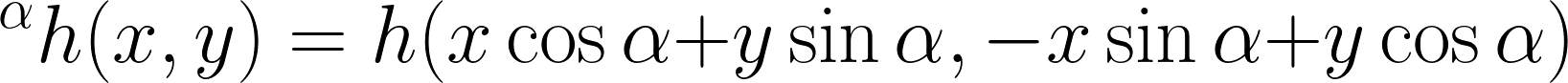 by linear combinations of functions from a fixed set, say
by linear combinations of functions from a fixed set, say 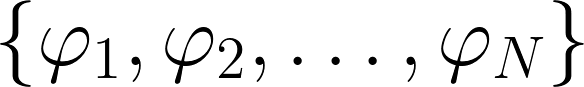 . That is to say, we are interested in minimising the following average approximation error
. That is to say, we are interested in minimising the following average approximation error
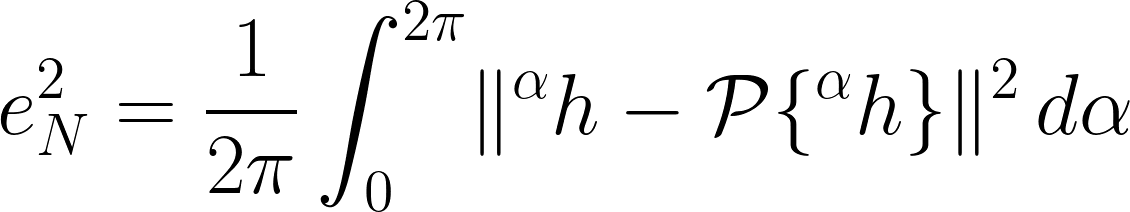
where 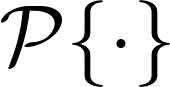 computes the orthogonal projection onto the span of the basis. This minimisation leads to the following rotation-covariant linear expansion, which we name Fourier-Argand representation,
computes the orthogonal projection onto the span of the basis. This minimisation leads to the following rotation-covariant linear expansion, which we name Fourier-Argand representation,
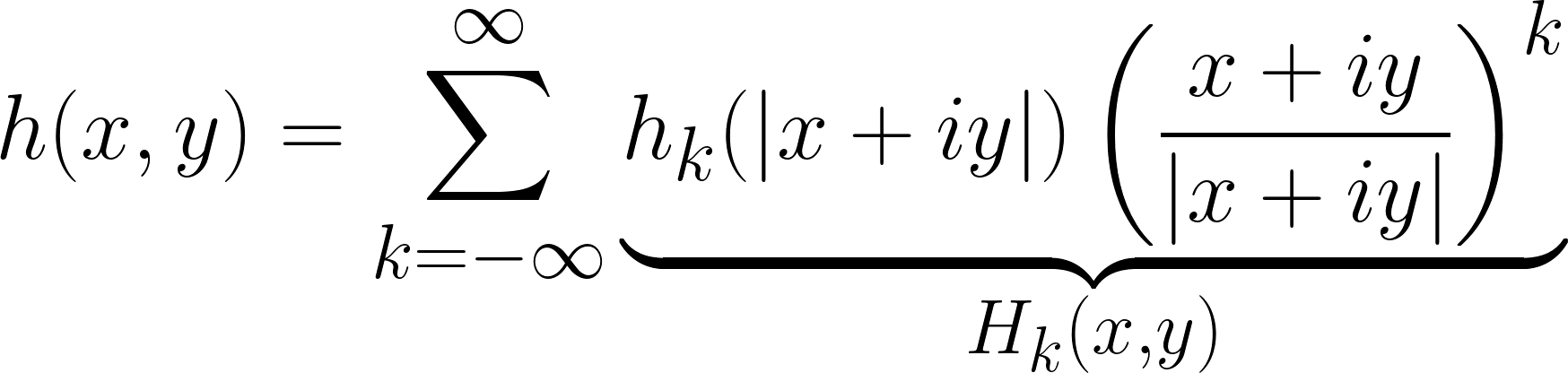
Each term of this expansion is rotation-covariant, in the sense that rotating each basis function amounts to multiplying it by a (complex) scalar, i.e., 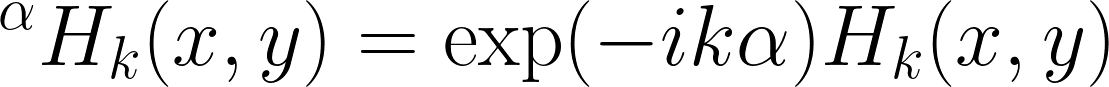 .
.
A few terms are sufficient to form a very accurate approximation to heavily elongated (high directional selectivity) functions while being readily steerable. See the figure below: (left) an elongated Gaussian (aspect ratio 1:10), (right) 10-term Fourier-Argand approximation.
 |  |
| Elongated Gaussian | 10-Term Fourier-Argand Approximation |
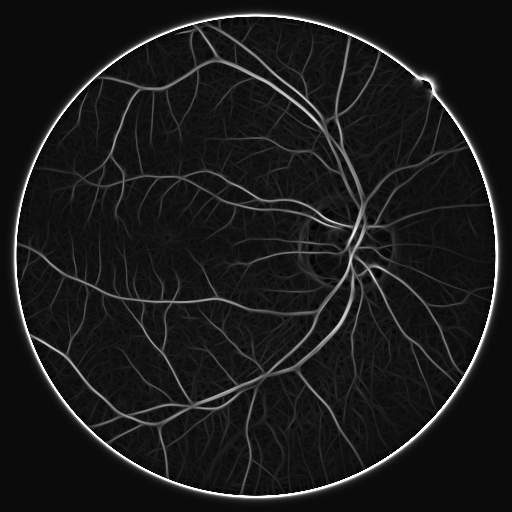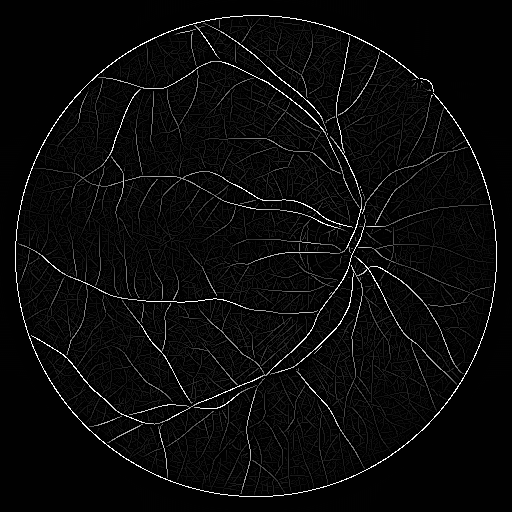
The representation allows us to efficiently detection image local structures. See the figure below for an example on ridge-like blood vessel detection.
 |
 |
 |
| Retinal Image | Filter Response | Detection Result |
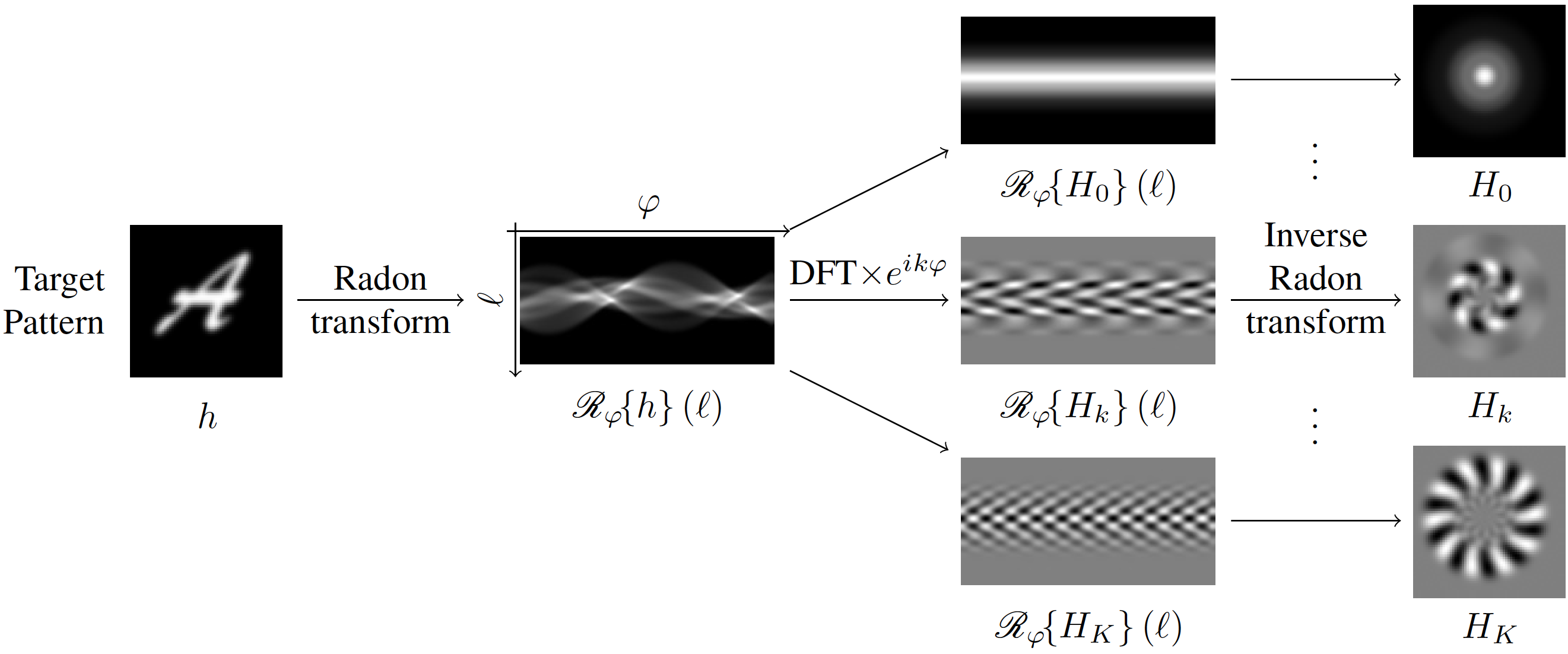
We also show how the Fourier-Argand representation of arbitrary patterns can be obtained using the Radon transformation:
References
| [1] Zhao, T. & Blu, T.,"The Fourier-Argand representation: an optimal basis of steerable patterns", IEEE Transactions on Image Processing, Vol. 29 (1), pp. 6357–6371, December 2020. |
Software for download
- The Matlab code implementing the Fourier-Argand representation is available here (2.5MB). Details on how to use this software: readme.txt.