Complex Wave Retrieval and Phase Restoration

Gang Luo and Thierry Blu

Outline

Digital holography is used to reconstruct complex waves and has a variety of applications, ranging from metrology to biological label-free quantitative imaging. The problem is to retrieve the complex-valued "object wave" 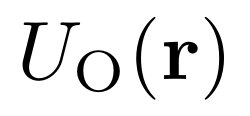and the complex-valued amplitude of the "reference wave" 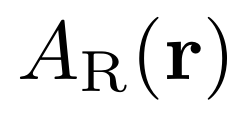from an interferogram modeled as 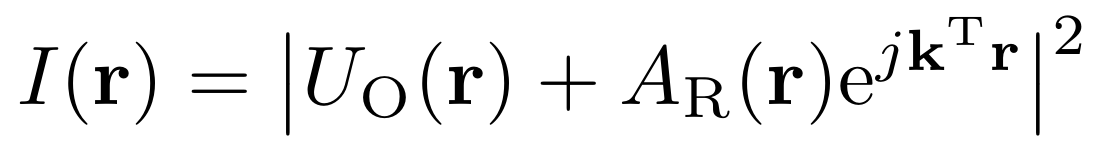. To solve this ill-posed problem, restrictive hypotheses on the object wave (e.g., bandwidth limitations) are usually made, whereas the reference wave is assumed to be known (e.g., from the acquisition of an additional interferogram without the object).

Here instead, we propose to estimate both the object wave and the reference wave from a single interferogram. This is achieved by parametrizing them adequately

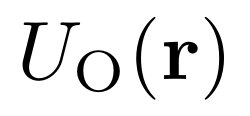• is bandlimited in some (large) frequency band
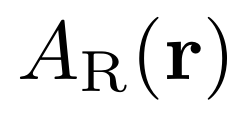• is bandlimited in some (narrow) frequency band

and by minimizing the mean square difference between the (square root) raw interferogram and this parametric model:

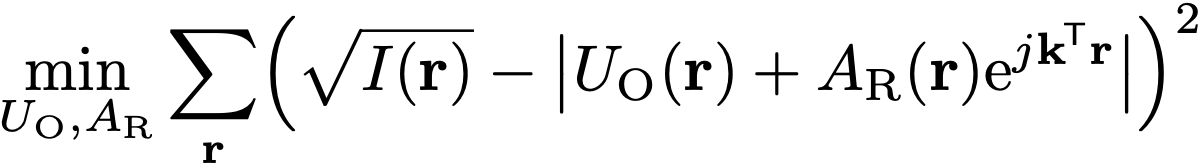
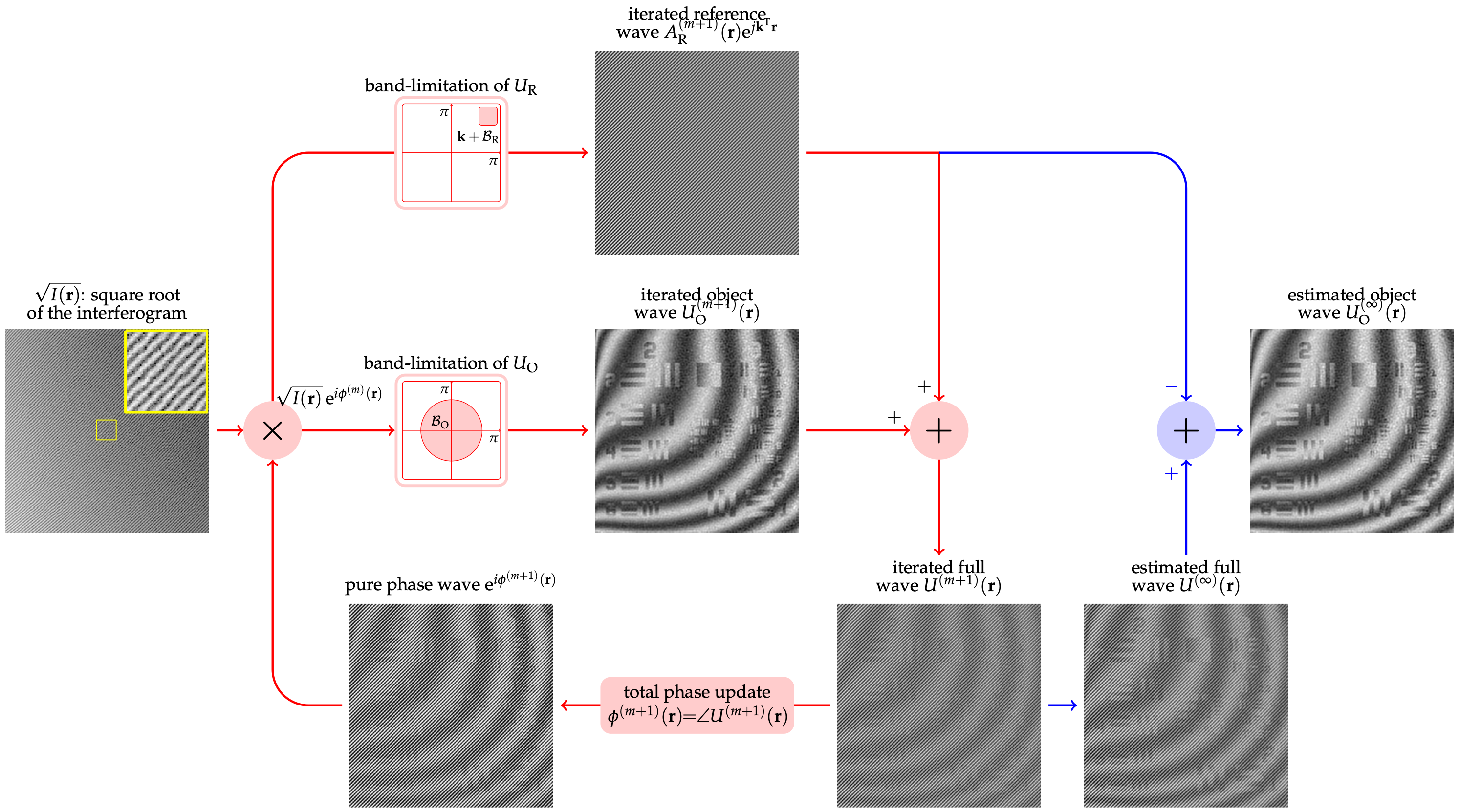
We choose an MM (majorization-minimization) strategy to address this optimization problem, leading to the efficient iterative algorithm depicted below (typically less than 10 iterations):

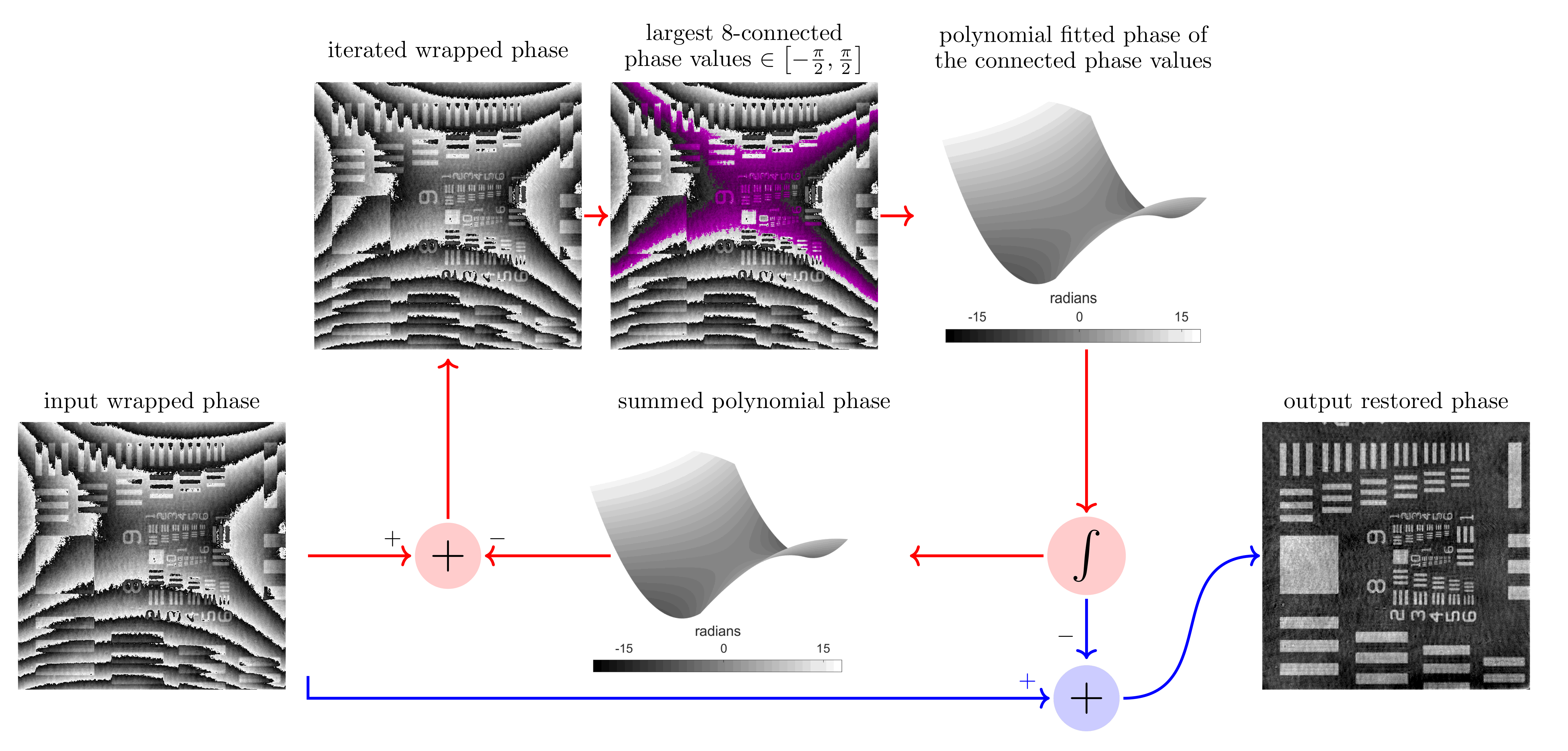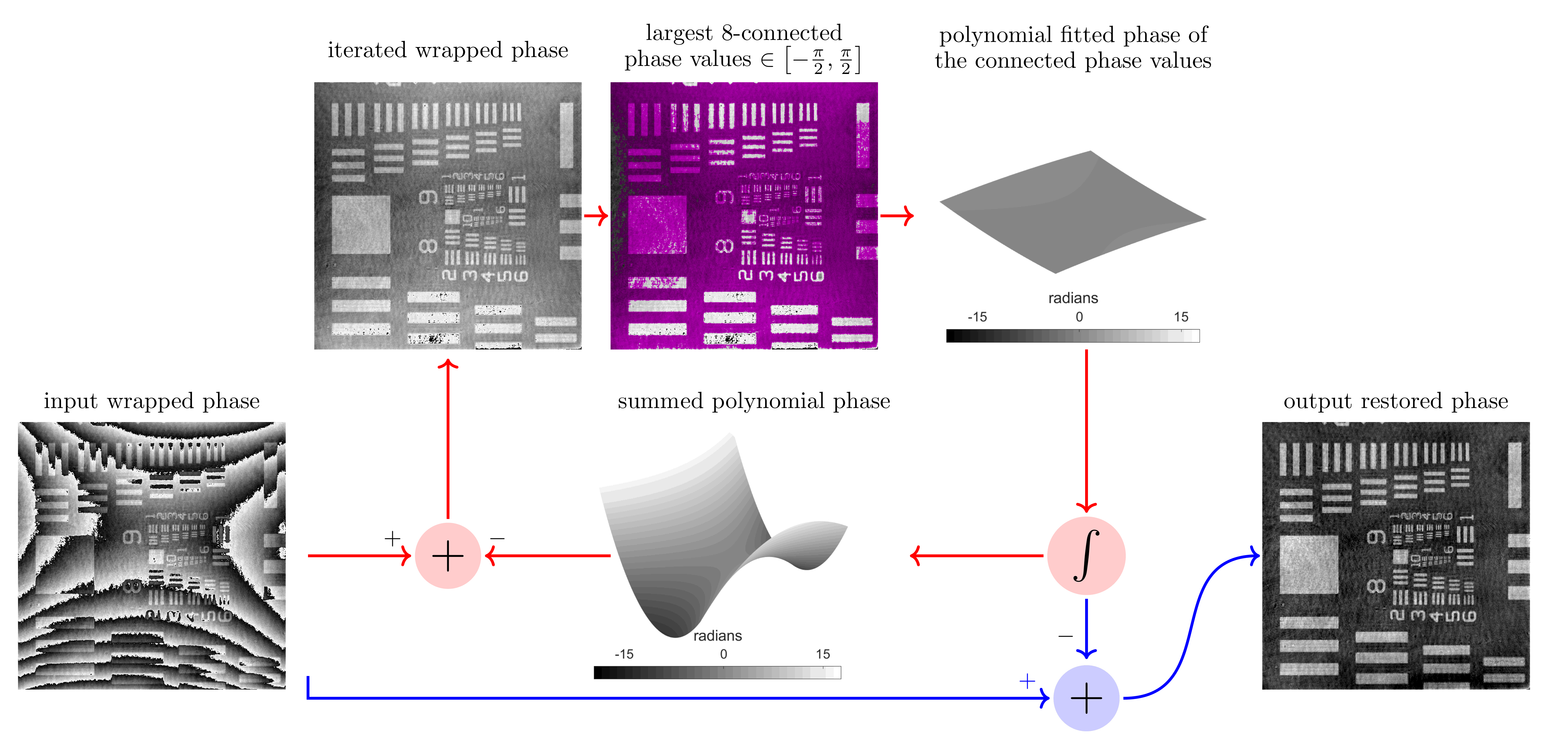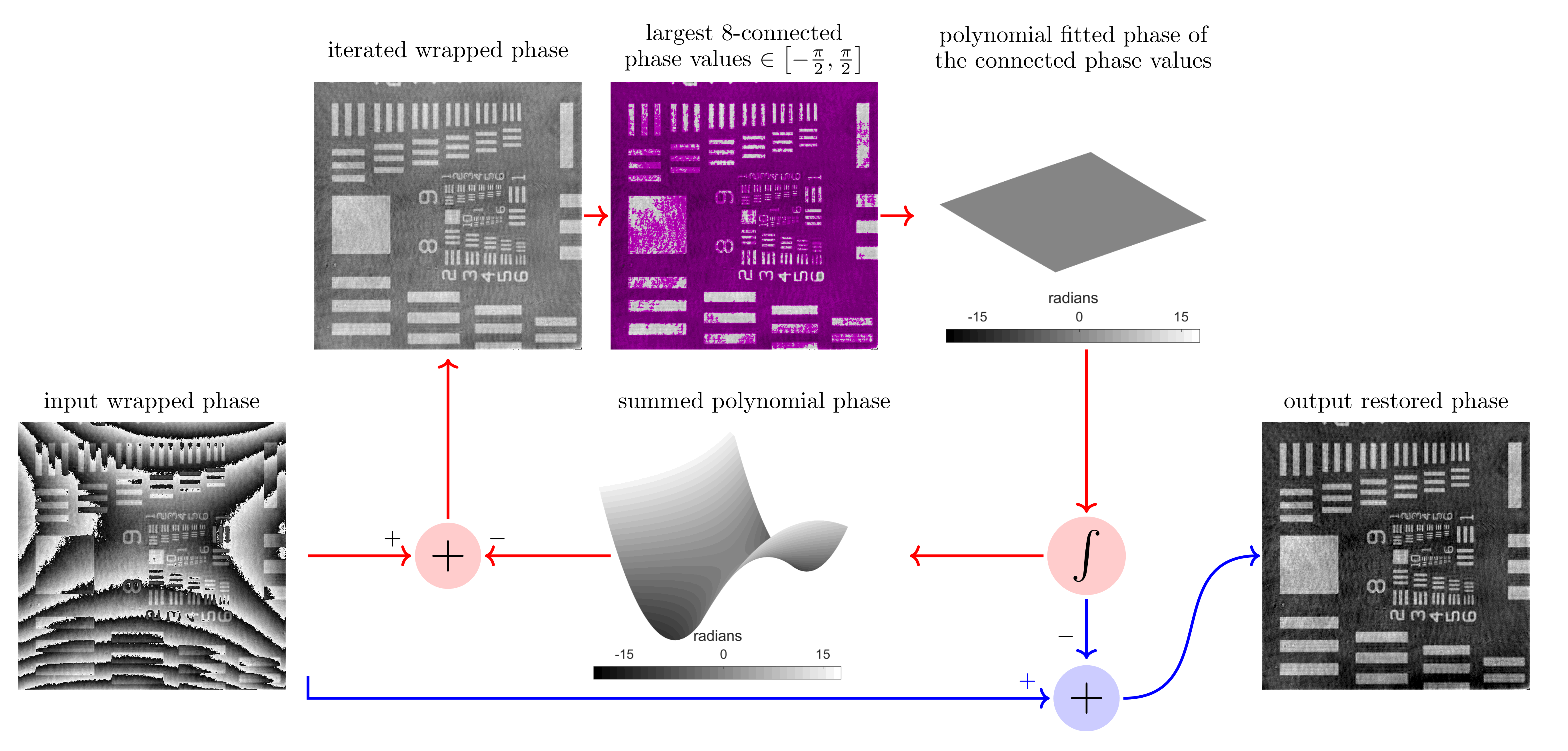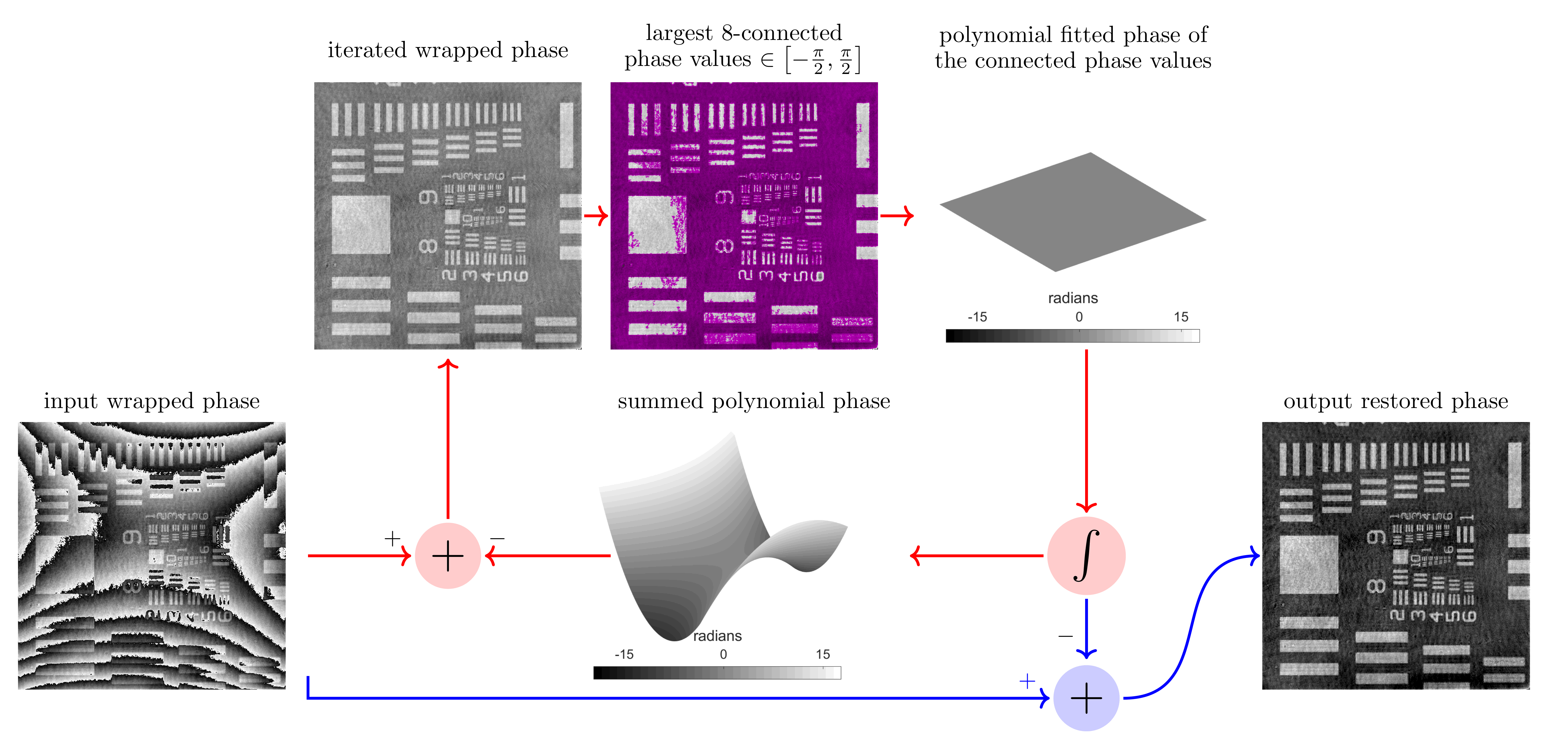
The retrieved object wave is usually corrupted by slow phase variations (caused by optical aberrations and inaccurate estimation of the reference phase) of large amplitude (>2π), which calls for a phase restoration step. Modelizing this phase distortion as a 2D polynomial of low degree (typically, ≤5), we have developed an efficient morphology-based algorithm that does not resort to phase unwrapping (usually slow) as depicted in the following animated flow chart:

Advantages of this work:

• single-frame acquisition only;
• significant overlap between the frequency bands (twin images and zeroth order);
• object bandwidth up to (about) half the bandwidth of the interferogram;
• realistic object vs reference amplitude ratio (e.g., between 0.2 and 2).

Example of object phase reconstruction from an interferogram: (top) USAF phase target; (bottom) Tobacco BY2 cell.

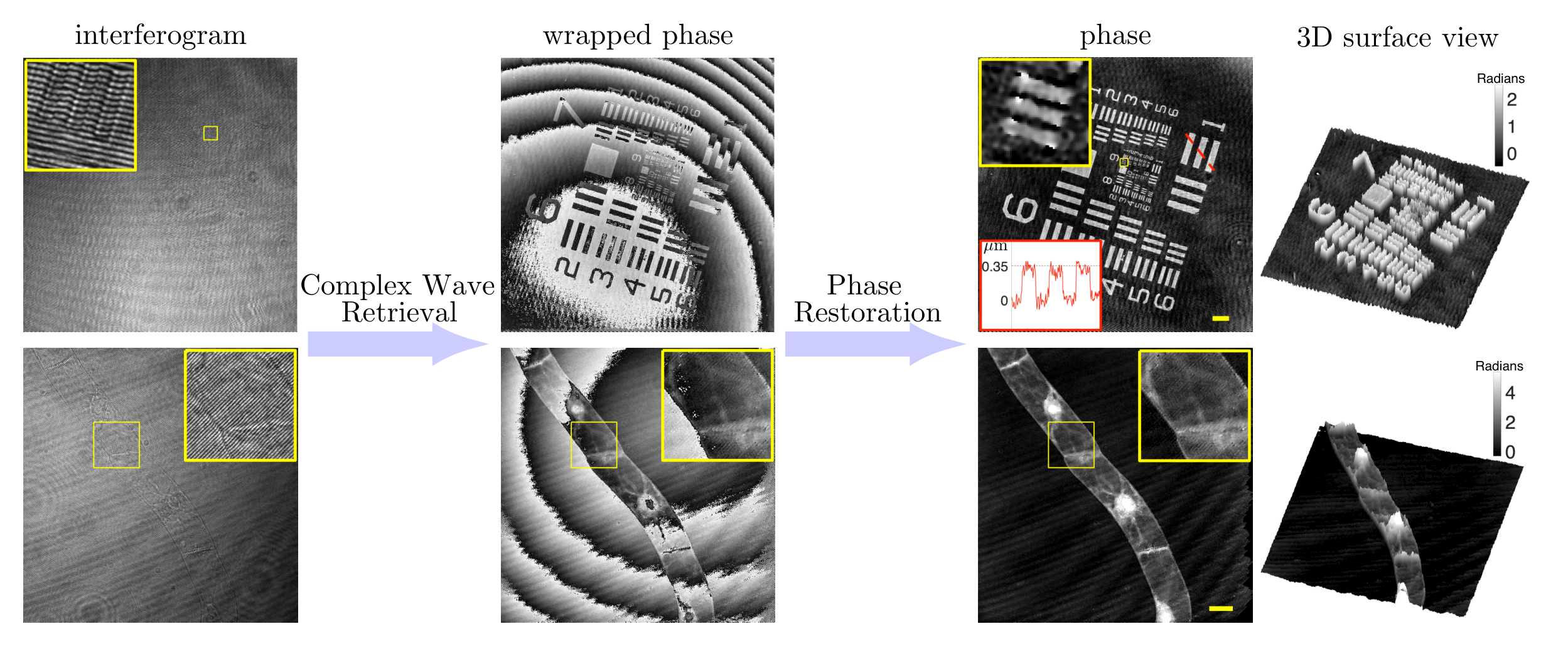
Reference

G. Luo, Y. He, H. Shu, R. Zhou & T. Blu,"Complex Wave and Phase Retrieval from A Single Off-Axis Interferogram", Journal of the Optical Society of America A, Vol. 40 (1), pp. 85-95, January 2023.

Matlab Software

The Matlab codes of the complex wave retrieval and phase restoration algorithms are available here (220KB). Details on how to use this software: README.txt.

Conditions of use — You are free to use this software for research purposes, but you should not redistribute it without our consent. In addition, we expect you to include an adequate citation and acknowledgment whenever you present or publish results that are based on it.